Trie

Please trie hard

Introduction

The second to last part will be dedicated to Tries. In this part, I’ll trie to explain what are their benefits, and why should we care about them.

Trie is a very specific type of tree that you’ve definitely encountered in some form. Why? Well, not because you’ve worked with it, no. But because you’ve used something that is built on top of it. Specifically, Google. Or any autocomplete really.

Have you ever wondered how autocorrect or autocomplete works? Me neither! Nevertheless, I’ll shove it up your brain so you will know what’s in your phone!

A Trie is a tree structure ideal for text-based features. Autocomplete and autocorrect are great examples of it.

In contrast to other trees, Trie doesn’t have a root. Or rather - the root doesn’t hold a value.

After talking a little about trees already, let’s take a look at a couple words and see how we could make a tree out of it:

Autocomplete
Autocorrect
Automaton
Algebra

Now, what can we do with the words? Well, not much actually. Because tries are more about the characters. Now, if you split it into characters, you may see where I am going:

Autocomplete: a -> u -> t -> o -> c -> o -> m -> p -> l -> e -> t -> e
Autocorrect: a -> u -> t -> o -> c -> o -> r -> r -> e -> c -> t
Automaton: a -> u -> t -> o -> m -> a -> t -> o -> n
Algebra: a -> l -> g -> e -> b -> r -> a

And from the individual characters, we could build a tree. It’s not complete, or balanced. But it certainly is a tree!

But how would that help us? Well, if we consider google, consider this feature:

Autocomplete returns top 10 most searched items based on what user is typing

Now, that’s great! But how would we know where to filter? We could send this to DB and fetch:

select * from autocomplete where query like '{myQuery}%' order by asc

But that would be searching across all queries, not to mention the system design issues if you have multiple databases.

We could use a trie for that instead.

Whenever a user is typing, only navigate through the tree, effectively removing A LOT of other options

Now, as for the top 10 most searched, we could keep these cached:

When user types “auto”, based on analytics, we may know that:
- “autocorrect” was searched for 100 times
- “autocomplete” was searched for 50 times
- “automaton” was searched for once
- We would cache these results in the nodes

But I’m getting ahead of myself. It’s better described in the following image:

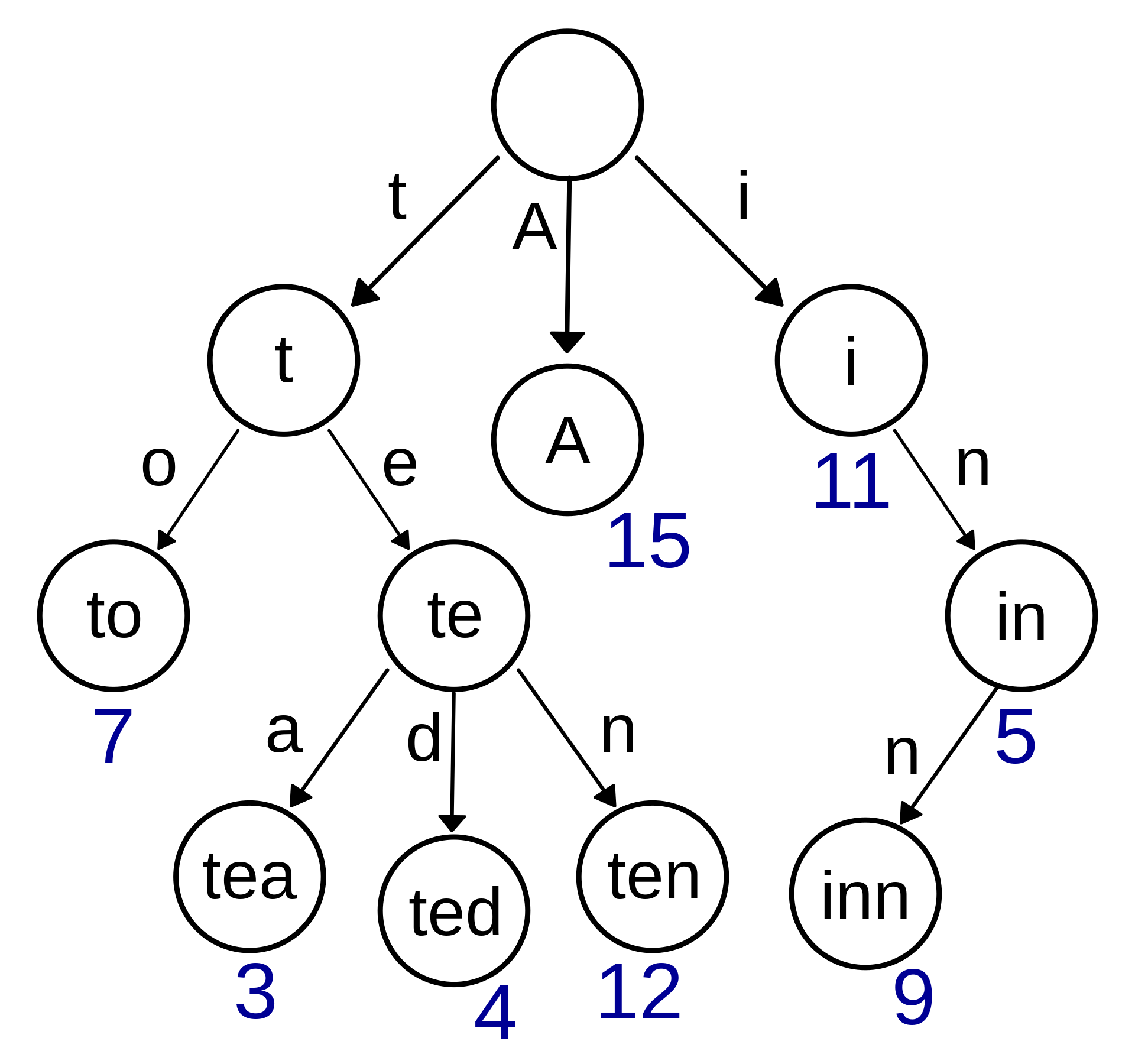
Note that each leaf has a value that’s associated with it. We could have this value cached on individual nodes level:

The top 2 searched for “t” node would be cached “to” and “ten”

Anyways, let’s build a Trie!

Operations

Trie has the following operations in the simplest form:

insert
search

There is no deletion or traversing, because they don’t make sense. We don’t want to remove previously created words, neither do we want to go through all of them.

For searching, an input will be a word (or a partial word) to search for
- We will iterate over input string and move down the trie as long as there are nodes
For inserting, an input is again a word
- We’ll go through the word, creating a trie node if it doesn’t exist

class TrieNode {
    children = {};
}

class Trie {
    rootNode = new TrieNode();

    search(word) {
        let currentNode = this.rootNode;
        for (let i = 0; i < word.length; i++) {
            const char = word[i]; 
            if (currentNode.children[char]) currentNode = currentNode.children[char];
            else return null;
        };
        return currentNode;
    }

    insert(word) {
        let currentNode = this.rootNode;
        for (let i = 0; i < word.length; i++) {
            const char = word[i]; 
            if (currentNode.children[char]) currentNode = currentNode.children[char];
            else {
                currentNode.children[char] = new TrieNode();
                currentNode = currentNode.children[char];
            }
        };
        currentNode.children["*"] = new TrieNode();
        return currentNode;
    }
}

Now, if you look at the insertion, there’s one more thing - ”*“. That’s because it means there can be any words after this. We don’t keep the entire dictionary somewhere, and new words are always being made up. That basically implies it.

And we’re done with Trie. Kind of. We’ve created all the operations. Now, everything is depending on the use cases.

Autocomplete

I’ve mentioned on the start that it’s good for text-based features. Let’s create autocomplete together.

Autocomplete with Tries is fairly simple:

We get a partial word from the user
We’ll return to him words already typed in our autocomplete

So, consider the following:

const trie = new Trie()
trie.insert('cat');
trie.insert('catnip');
trie.insert('catnap');
trie.insert('ace');
trie.insert('act');

We have a trie that has some words in it. Now, let’s consider we want an autocomplete:

When we type in ca, we’ll receive an array of cat, catnip, catnap
When we type in ac, we’ll receive an array of ace, act

So, what we need to do is create a function that retrieves these words.

function getAllPossibleWords(node = null, word = "", words = []) {
    const currentNode = node || this.root;
    const children = Object.keys(currentNode.children);
    children.forEach((key) => {
        if (key == "*") words.push(word);
        else {
        this.getAllPossibleWords(currentNode.children[key], word + key, words);
        }
    });
    return words;
}

Now, here we are using recursion on the Trie.

We receive a specific node on which we are searching for
We pass the partial word down
We fill the passed array with all complete words
If the key is a star, then we’ll return the word as is (as there are no children under star)

And now, autocomplete is simple. We’ll just combine functions we already have:

we search for the node based on text
we receive the word from the user
we fill all possible words using the above function

So, it’ll look like this:

function autocomplete(word) {
    const node = this.search(word);
    if (!node) return null;
    return this.getAllPossibleWords(node, word);
}

And that’s it for autocomplete!

Autocorrect will be pretty much the same thing, except:

We have a word we want to correct
We want to find the closest match

So, to do so, we could do:

function autocorrect(toCorrect) {
    let node = this.search(toCorrect);
    if (node) return toCorrect;
    while (!node) {
        toCorrect = toCorrect.slice(0, toCorrect.length - 1);
        node = this.search(toCorrect);
    }
    const words = this.getAvailableWords(node, toCorrect);
    return words[0];
}

With the above function, we’ll search if the word we want to correct exists. If not, we’ll progressively move to the top.

This will be result in catp being shortened to cat, searched for, and then returned!

Code

The code written here in total is:

class TrieNode {
  children = {};
}

class Trie {
  root;
  constructor() {
    this.root = new TrieNode();
  }

  search(word) {
    let node = this.root;
    for (let i = 0; i < word.length; i++) {
      const char = word[i];
      if (node.children[char]) node = node.children[char];
      else return null;
    }
    return node;
  }

  insert(word) {
    let node = this.root;
    for (let i = 0; i < word.length; i++) {
      const char = word[i];
      if (!node.children[char]) node.children[char] = new TrieNode();
      node = node.children[char];
    }
    node.children["*"] = new TrieNode();
    console.log(node.children);
    return node;
  }

  autocomplete(word) {
    const node = this.search(word);
    if (!node) return null;
    return this.getAllPossibleWords(node, word);
  }

  getAllPossibleWords(node = null, word = "", words = []) {
    const currentNode = node || this.root;
    const children = Object.keys(currentNode.children);
    children.forEach((key) => {
      if (key == "*") words.push(word);
      else {
        this.getAllPossibleWords(currentNode.children[key], word + key, words);
      }
    });
    return words;
  }
}

const trie = new Trie();
trie.insert("cat");
trie.insert("catnip");
trie.insert("catnap");
trie.insert("ace");
trie.insert("act");
trie.autocomplete("ac");

Feel free to play around with it!

Summary

In this piece, I’ve gone through tries. A third data structure we’ve discovered after binary search trees and heaps.

Tries are very solid data structure that can be used in many text-based features.