Heaps

Trees but... arrays?!

Introduction

When working with JavaScript, I’ve often seen the error JavaScript Heap Out of Memory Error. I’ve never known what a heap is.

In short, it’s a tree. Kind of.

In previous part, we’ve had binary search tree - that is, a binary tree that is optimized for searching.

Values in left children are lesser than current value
Values in right children are greater than current value

Now, notice how I’ve emphasized the binary tree. Because BST is just a form of binary tree. Heap is another kind.

A binary tree is in essence very simple:

Has a root level
Each node has 2 children

So, if we would have a completely balanced tree, we could have something like:

first level - root - 1 node
second level - root children - 2 nodes
third level - 2 * 2 - 4 nodes

You may see where I’m going with this. Binary tree has levels of power of 2. If a binary tree has 10 levels and is balanced, it’ll have a maximum of 2^10 nodes (2^0, 2^1, 2^2, … 2^10)

Now, another term for this is complete binary tree.

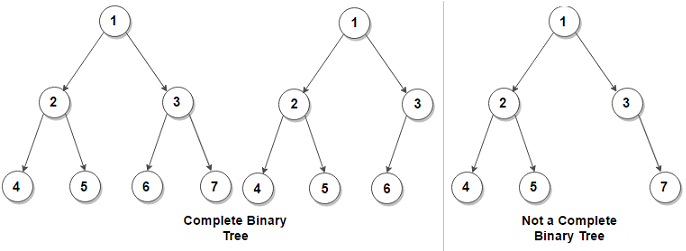
In other words, if we go by leaves, we’ll see that there is no missing value. In the incomplete tree, we have a missing leaf 3.

How does this help us heaps and why should we care? Well, let’s investigate!

Making trees into arrays

As the subtitle suggests, we’re not gonna use trees as we used to with BST. Instead, we’ll use an array. And here comes the important bit:

Heaps must be complete binary trees

Now, consider you have the following array: [1,2,3,4,5,6]

If you look at it, you could try to put it into a tree:

1
- 2
  - 4
  - 5
- 3
  - 6

And you would be right! That’s exactly what a heap is. The only difference is that we don’t do links between nodes, and we effectively go by levels (note the number 4 is a child of 2)

So, let’s create a simple heap:

class Heap { 
    data = [];

    getRootNode = () => this.data.at(0)
    getLastNode = () => this.data.at(-1)
}

Now, that’s a simple heap. It’s just a wrapper around array. But how does this help us?

Well, consider the array above:

we are at the root - index 0
we want to get to the left child - index 1

How do we do that? Well, we could increment it. But what if we want to go left even more? Think about the indices in the array

[1,2,3,4,5,6,7,8,9]

root - 0 (value 1)
left child - 1 (value 2)
lefter child - 3 (value 4)
lefter lefter child - 7 (value 8)

Now, we’re getting somewhere. Notice the pattern in there. Now, look at the question above and consider:

we want to move from root level to 3th level
The indices are 0, 1, 3, 7

With the indices it’s a little harder to see, but we see the binary part. To get the left child, we just do index * 2 + 1!

root level: 2 * 0 + 1 => 1
1st level: 2 * 1 + 1 => 3
2nd level: 2 * 3 + 1 => 7
3rd level: 2 * 7 + 1 => 15

In fact, we can traverse the tree with simple multiplication! The same goes for right child - instead of 1, we add 2:

root level: 2 * 0 + 2 => 2
1st level: 2 * 2 + 1 => 5
2nd level: 2 * 5 + 1 => 11

Note that the above is moving only left/right. If we wanted to go left/right/left, we’d need the addition to be 1, 2, 1 respectively.

And finally, how do we get the parent? Well, let’s take a look at the above example:

3rd level is 11
2st level is 5
1st level is 2
root level is 1

Well, we’re again doubling - except backwards! We’re dividing by 2! If we divide 11 by 2, we get 5.5. Cut off the remainder and we have it!

But wait, there’s one more trick here. Consideer the following heap: [0,1,2,3,4,5,6,7,8,9,10,11,12]. It’ll look like:

0
- 1
  - 3
    - 7
    - 8
  - 4
    - 9
    - 10
- 2
  - 5
    - 11
    - 12
  - 6

If you take a look, it still works for 11. However, it doesn’t work for 10. If you Math.floor(10 / 2), you will still get 5.

But as seen above, it’s actually 4. We need to have subtract one in here. The final function is:

So, the function here is Math.floor((index - 1) / 2)

So, let’s continue with our Heap!

class Heap { 
    data = [];

    getRootNode = () => this.data.at(0)
    getLastNode = () => this.data.at(-1)
    getLeftChildIndex = (parentIndex) => (parentIndex * 2) + 1;
    getRightChildIndex = (parentIndex) => (parentIndex * 2) + 2;
    getParentIndex = (childIndex) => Math.floor(childIndex - 1) / 2
}

And that’s it. We’ve created iur heap processing. But we still can’t insert or delete, can we?

Well, we’re not done yet. The problem is - insertion and deletion depends on the type of heap.

Min Heap
Max Heap

Now, you can easily view this as a sorted array:

min heap -> node is lower than its children
max heap -> node is higher than its children

To insert and delete, we’ll use a technique called trickling. Because of this, we’ll allow insertion and deletion to be O(log N) rather than O(N) with regular arrays.

Trickling

When we insert something in the table, we’re working cleverly with the indices. Consider the following heap: 2,3,4,5,6,7,8,9,10

Now, this can we written also as:

2
- 3
  - 5
    - 9
    - 10
  - 6
- 4
  - 7
  - 8

But wait. There’s an issue here. Because the definition of min-heap is that the node is lower than its children. That’s an invalid min-heap! While I call it a heap, we can’t use it for this example.

Now that is important because of the insertion and deletion! Consider the following image:

If we insert at the end the value 19, we don’t need to move it anywhere. But if we insert a value 5, we need to move it to the top and swap them all.

So, to trickling:

So, we’ll trickle the node to the top! What do I mean by that? Well, let’s take a look:

We take the node
We know how we can get the parent
While the parent is higher, we’ll be swapping the elements

Let’s quickly create a min heap insertion:

class MinHeap extends Heap {
    insert(value) {
        this.data.push(value);
        let index = this.data.length - 1;
        let parentIndex = this.getParentIndex(index);
        while (this.data[parentIndex] > this.data[index]) {
            const temp = this.data[index];
            this.data[index] = this.data[parentIndex];
            this.data[parentIndex] = temp;
            index = parentIndex;
            parentIndex = this.getParentIndex(index);
        }
    }
}

Now, for max heap, it’s gonna be pretty much the same. The condition is going to be different:

class MaxHeap extends Heap {
    insert(value) {
        this.data.push(value);
        let index = this.data.length - 1;
        let parentIndex = this.getParentIndex(index);
        while (this.data[parentIndex] < this.data[index]) {
            const temp = this.data[index];
            this.data[index] = this.data[parentIndex];
            this.data[parentIndex] = temp;
            index = parentIndex;
            parentIndex = this.getParentIndex(index);
        }
    }
}

If you look closely, both codes are exactly the same, with the condition being swapped.

And that’s it for insertion!

Push to the end of array
Get current index
Get parent index
While parent is greater than child, swap elements and calculate next index

Deletion

Now, deletion is a little weird. To understand deletion, let’s talk a little about the use cases. Heaps are often used in priority queues. What that means is consider you have 80 tasks to do. Each has a priority. I can use a max heap for that:

The task with highest priority will be the root of the heap
The next highest priority task will be moved to the top

So, when deleting from a heap, we’ll always remove from the top. We won’t be removing individual branches.

Now, you could see this as removing from top of array, and that would be simple. But with heaps, we’re looking for a fast solution. So, what we’ll do is - we will replace the top element, but not remove it.

How will we do that? Well, remember trickling? We were moving upwards. We’ll do exactly the same in here.

We will “remove” the last element
We will trickle this last element up
The first element will be effectively removed as it’s replaced with another value

Now, there’s one more step in here. We need to consider both parts of the node and moved that one up.

So, let’s quickly do that for min-heap:

class MinHeap extends Heap {
    delete() {
        const lastValue = this.data.pop();
        let index = 0;
        this.data[index] = lastValue // replace the first item, effectively removing it
        let leftChildIndex = this.getLeftChildIndex(index);
        let rightChildIndex = this.getRightChildIndex(index);
        while (
            this.data[leftChildIndex] < this.data[index] || 
            this.data[rightChildIndex] < this.data[index]
        ) {
            const temp = this.data[index];
            const lesserNodeIndex = this.data[leftChildIndex] < (this.data[rightChildIndex] || Infinity)
                ? this.data[leftChildIndex] 
                : this.data[rightChildIndex]
            this.data[index] = this.data[lesserNodeIndex]
            this.data[lesserNodeIndex] = temp;

            leftChildIndex = this.getLeftChildIndex(index);
            rightChildIndex = this.getRightChildIndex(index);
        }
    }
}

And that’s pretty much it! We:

compare left and right children to see where we’re going
We swap the current node with smaller node
We repeat until there are no lesser elements

Again, for max-heap, it’s exactly the same thing. The only difference is the condition!

class MinHeap extends Heap {
    delete() {
        const lastValue = this.data.pop();
        let index = 0;
        this.data[index] = lastValue;
        let leftChildIndex = this.getLeftChildIndex(index);
        let rightChildIndex = this.getRightChildIndex(index);
        while (
            this.data[leftChildIndex] > this.data[index] ||     // swapped condition
            this.data[rightChildIndex] > this.data[index]       // swapped condition
        ) {
            const temp = this.data[index];
            const lesserNodeIndex = this.data[leftChildIndex] > (this.data[rightChildIndex] || -Infinity) // - Infinity
                ? this.data[leftChildIndex] 
                : this.data[rightChildIndex]
            this.data[index] = this.data[lesserNodeIndex]
            this.data[lesserNodeIndex] = temp;

            leftChildIndex = this.getLeftChildIndex(index);
            rightChildIndex = this.getRightChildIndex(index);
        }
    }
}

Summary

Heaps are very effective priority queues and in this part, we’ve investigated 2 of them:

Min-Heap (all nodes are lesser than their descendants)
Max-Heap (all nodes are greater than their descendants)