Binary Search Trees

Binary Search in Trees!

Introduction

We’re now moving to trees where recursion will really shine. So, let’s talk a bit about trees before we dive deep into it.

In arrays, I’ve shown a basic binary search, always halving the array, allowing for O(log N) complexity in search.

Binary search trees make use of that. You could say they’re a special case of linked list. Where linked list had a following single node, binary search trees have 2 following nodes

So, how can a basic binary search look like? Well, in code, it’d look something like this:

const bst = {
    root: {
        value: 10,
        leftNode: {
            value: 5,
        },
        rightNode: {
            value: 15
        }
    }
}

In essence, it’s a simple tree.

it has a root node
every node has reference to leftNode and rightNode
leftNode value must be lesser than current node
rightNode value must be greater than current node

That’s pretty much all the rules. But there are some limiting factors

Let’s talk trees

Consider that you have a tree of 3 levels. We’d have a total of 7 nodes (1 + 2 + 4)

root
root-left, root-right
root-left-left, root-left-right, root-right-left, root-right-left

If you were to search in this tree, for any value, it’d take you 3 steps (the amount of levels).

But would it? Sometimes, your tree can be a little weird. Imagine that for some reason, all values are greater than the root node. In such a case, the amount of levels would be 7, as well as the amount of nodes. See following image:

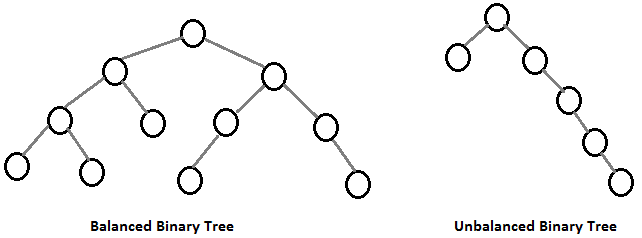
That would be unfortunate for multiple reasons:

The traversal is usually using recursion. With many levels comes massive space complexity
- For 1000 nodes, finding the desired node:
  - Unbalanced - 1000 operations, 1000 function calls (O(n))
  - Balanced - 10 operations, 10 function calls (O(n log n))

Some more terminology includes predecessor and successor

the current node has a value.
the predecessor is the node with value closest to the current that is lesser
the successor is the node with value closest to the current that is greater

With binary trees, these are fairly easy to find

predecessor is one node to the left, then all the way right
successor is one node to the right, then all the way to the left

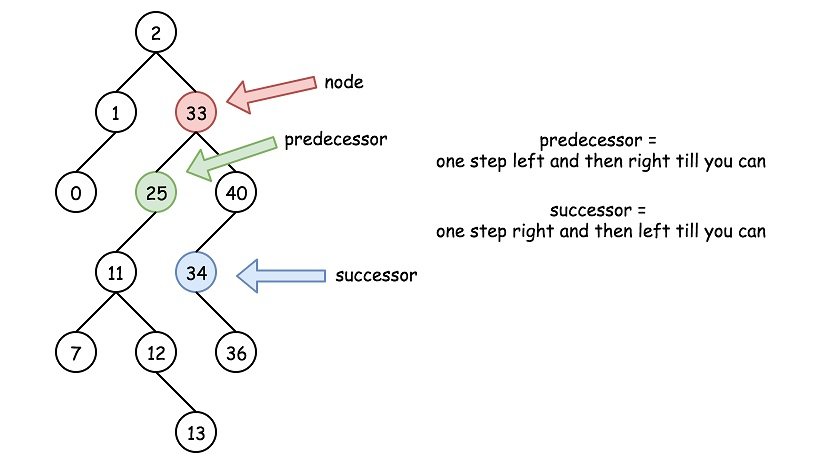
And finally, traversing a tree. To go through a tree, we have 2 options:

Go by levels (Breadth-First Search)
Go as deep as you can (Depth-First Search)

We’ll implement them both eventually, but that’s enough of theory for now.

BST versus other data structures

Before going deep into building a BST, let’s recap the benefits of BST:

Arrays can be unsorted and operations in them can be relatively slow
Sorting arrays is useful when we are working with them
- Sorting takes O(N log N)
- Insertion and deletion take O(N)
Hash tables are great, but unordered. While they are O(1) for insertion, deletion and search, the order is not given

With those concepts above, we’re getting to the gist of it. Order. If we rely on sorted data, it’s worht creating a data structure that is fast for addition and removal of data, as well as searching. Binary Search Tree is exactly that.

In worst case (completely unbalanced tree), binary search tree is just a doubly linked list.

And finally, an interesting fact I found while searching online. Morse code can be written in binary search tree!

The values are dots and dashes
When moving left, use dot
When moving right, use dash

BST Operations

So, let’s deep dive to BST operations. We have:

insertion
search (find value)
traverse (move through all)
deletion

So, let’s start with defining a node:

class TreeNode {
    leftChild;
    rightChild;
    value;
    
    constructor(value, left, right) {
        this.value = value;
        this.leftChild = left;
        this.rightChild = right
    }
}

A simple tree node has basically 3 references:

value
left child (values smaller than current)
right child (values greater than current)

Now, when we go inserting a node, we need to search for it first. Kind of.

Each node takes care about the insertion for its own. Since we have a lot of nodes, we’ll move deeper down:

insert(value) {
    if (this.value === value) {
        console.error("Value already exists");
        return null;
    }
    if (value < this.value) {
        if (this.leftChild) {
            this.leftChild.insert(value);
        }
        else {
            this.leftChild = new TreeNode(value)
        }
    }
    if (value > this.value) {
        if (this.rightChild) {
            this.rightChild.insert(value);
        }
        else {
            this.rightChild = new TreeNode(value)
        }
    }
}

The above code is fairly simple as it’s a bunch of if statements:

If value already exists, we won’t do anything
If the value is lesser than of current node, we’ll move to the left
Otherwise, move to the right
Create node when no node is connected

Now, to try this out, let’s traverse it. Traversing is basically going through the entire tree. Traversing is simple - we just move to next nodes:

traverse() {
    this.leftChild?.traverse()
    this.rightChild?.traverse()
}

Now, consider what you want to do with the value you’re traversing. Consider that you have the following tree:

25
- 15
  - 10
  - 20
- 35
  - 30
  - 40

What if you put a print call on the first line, last line, or in between? Well, let’s take a look:

traverse() {
    console.log(this.value); // 25, 15, 10, 20, 35, 30, 40
    this.leftChild?.traverse()
    console.log(this.value); // 10, 15, 20, 25, 30, 35, 40
    this.rightChild?.traverse()
    console.log(this.value); // 10, 20, 15, 30, 40, 35, 25
}

If you compare the logs in there, you can see that:

If you work with the print at the start, you’re printing them as you go through the tree. This is “Pre order” traversal
If you work with the print in the middle, you have a “In Order” traversal. The values are listed as sorted
If you work with the value at the end, you’re traversing “Post Order”. You go to the most left leaf and go up from there.

This is better visible in the following example:

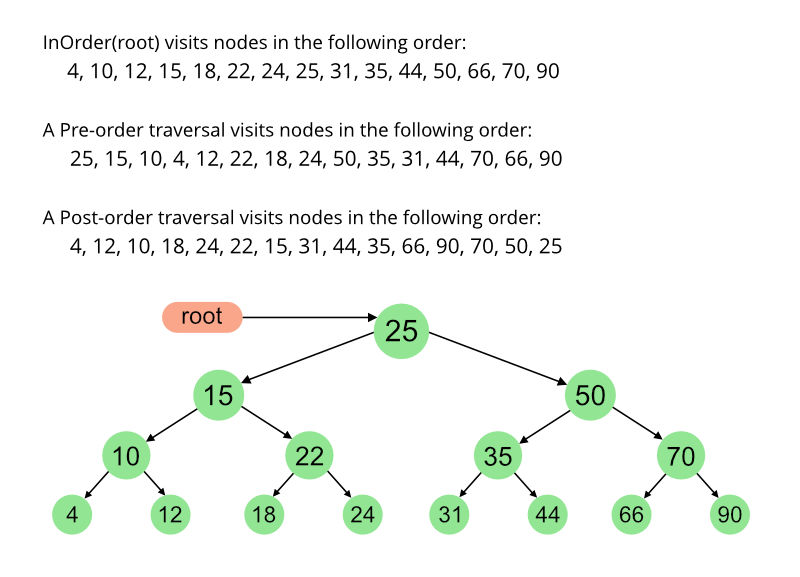
Let’s continue with finding a value, because this is where it really shines. This is very similar to insertion:

findNodeWith(value) {
    if (this.value === value) return this;
    if (value < this.value) return this.leftChild.findNodeWith(value)
    if (value > this.value) return this.rightChild.findNodeWith(value)
    return null;
}

The above function is a simple search

If value is found, return the current node
If not, go to the right or left, depending on size of the value
Return null if value can’t be found

Deletion

The most problematic part of binary search trees is deletion. As we’ve seen, insertion is easy:

To insert a value, we find the correct position. If value already exists, log error
To traverse, we go through all nodes recursively
To find a node, we halve the number of nodes every time we search by going only left/right depending on position

So, how do we delete a node? Well, here come the successor and predecessor nodes. First, let’s start with searching the node to delete:

delete(valueToDelete) {
    if (valueToDelete > this.value) this.rightChild = this.rightChild?.delete(valueToDelete)
    if (valueToDelete < this.value) this.leftChild = this.leftChild?.delete(valueToDelete)
    if (valueToDelete === this.value) {
        if (!this.leftChild) return this.rightChild;
        if (!this.rightChild) return this.leftChild;
        this.rightChild = this.rightChild.lift(this)
    }
    return this;
}

Now, that’s basically it for the delete itself. When we delete a node, we just find the node to delete and return it. The problem comes with replacing the node.

Now, if your IQ is on par with a the drawing sticks in a box of crayons, you may figure out what’s next

We find the successor node (one step right, all the way to the left)
We replace the current node with the successor

Why with the successor? Well, consider the following:

30
- 25
  - 20
  - 27
- 35
  - 33
    - 31
    - 34
  - 37

So, what happens if you delete the number 30? What node takes its place?

It still needs to be higher than the highest lowest value (27)
It still needs to be lesser than lowest highest value (31)

Well, the last point doesn’t exactly stand. Because we will use it as the next node. In the above example, we’ll replace the node 30 with node 31. Let’s see what happens:

31
- 25
  - 20
  - 27
- 35
  - 33
    - null
    - 34
  - 37

The binary tree is still intact. By replacing the node with successor, we’ve kept the order correct! We also need to relink existing links

So, let’s define ourselves a lift function!

lift(parentNodeToDelete) {
    if (this.leftChild) {
        this.leftChild = this.leftChild?.lift(parentNodeToDelete);
        return this;
    }
    parentNodeToDelete.value = this.value;
    return this.rightChild;
}

I invite you to try to draw the above code on a piece of paper, but basically:

lift is always called on a right node, therefore to find the successor, we move left (until there’s no higher left value).
We find the successor node, and set the value of the deleted node to the current on
We return the right child of this node (because there is no left child at this point)
- This is to relink the tree. All the child links are still intact, but we still need to connect them

Code

The entire code will look something like this:

class TreeNode {
  leftChild;
  rightChild;
  value;

  constructor(value, left, right) {
    this.value = value;
    this.leftChild = left;
    this.rightChild = right;
  }

  insert(value) {
    if (this.value === value) {
      console.error("Value already exists");
      return null;
    }
    if (value < this.value) {
      if (this.leftChild) {
        this.leftChild.insert(value);
      } else {
        this.leftChild = new TreeNode(value);
      }
    }
    if (value > this.value) {
      if (this.rightChild) {
        this.rightChild.insert(value);
      } else {
        this.rightChild = new TreeNode(value);
      }
    }
  }

  traverse() {
      console.log(this.value);
    this.leftChild?.traverse();
    this.rightChild?.traverse();
  }

  findNodeWith(value) {
    if (this.value === value) return this;
    if (value < this.value) return this.leftChild.findNodeWith(value);
    if (value > this.value) return this.rightChild.findNodeWith(value);
    return null;
  }

  delete(valueToDelete) {
    if (valueToDelete > this.value)
      this.rightChild = this.rightChild?.delete(valueToDelete);
    if (valueToDelete < this.value)
      this.leftChild = this.leftChild?.delete(valueToDelete);
    if (valueToDelete === this.value) {
        console.log(this.value)
      if (!this.leftChild) return this.rightChild;
      if (!this.rightChild) return this.leftChild;
      console.log(this.rightChild.value)
      this.rightChild = this.rightChild.lift(this);
    }
    return this;
  }

  lift(parentNodeToDelete) {
    if (this.leftChild) {
      this.leftChild = this.leftChild?.lift(parentNodeToDelete);
      return this;
    }
    parentNodeToDelete.value = this.value;
    return this.rightChild;
  }
}

Summary

Binary trees are extremely useful in computer science. A lot of programmes run them under the hood because of how fast the insertion, deletion and search is.

That being said, it can’t be used everywhere. We need to keep in mind the spacial complexity.

Imagine that we started at 1 and counted to 1000
During traversal, we’d call 1000 times, and we would perform a lot of operations
We are likely to hit recursion limits with unbalanced trees