The Big Oh Notation
How to measure algorithm speed
Introduction
So, I’ve finished writing system design interview. But it’s not the end. It’s time for data structures and algorithms now!
In software development, whenever we are creating a new feature, it’s important to choose the right data structure. For example, with autocomplete, it’d be very difficult for us to create it without Trie.
Now, I’m not gonna put links here, yet. We’ll investigate individual structures. But to give an idea on efficiency, consider an array:
- Reading an array on a specific index is constant
- Searching for a specific item is variable
- Is the array sorted?
- Which algorithm is used?
- Do we only want to retrieve first occurence or all?
- Inserting a specific item depends on the position
- At the end, O(1) - we only add 1
- At the beginning, O(n) - we need to add 1 and move all others
- Deleting a specific item depends on position
- At the end, O(1) - we only remove 1
- At the beginning, O(n) - we need to remove 1 and move all others
- On Set, it is similar to an array. Deleting is same. Inserting is different
- Set allows only unique values
- Set has to first be searched for the value before inserting
- Array will have faster insertion
It may look like we always want an Array, right? Inserting is slower. Deleting is same. Searching is same.
But what really is the question is: Is it more important for our code to have no duplicates, or faster insertion
So before I go forward, let me put an example of the importance:
- In code, we express what needs to be done by lines of code
- Effectively, every line of code we write is some kind of algorithms
- Algorithm basically means instructions to follow/steps to perform
- If we define unnecessary steps, the code will be slower
- With algorithms, we can reduce the complexity of code
Consider searching in an array:
- Take an unsorted array, find first item and return it
- We need to go one by one in the array and return the first item that matches our request
- Worst case scenario - we will find this item at the end of array
- If array has 1_000_000 items, we will perform 1_000_000 steps
- We could go from end, but if it is on the first index, we will still take N steps
- Take a sorted array, find first item and return it
- We have to take log2 N steps to find the item
- We look at the middle and see if what we are searching for is higher/lower.
- If lower, we’ll take the lower half do the same.
- If higher, we’ll take higher half and do the same.
- If found, we’ll return it
- If the array length is 1_000_000 and:
- we search for 500_000, we find it in the first step
- we search for 2, we find it in around 20 steps
- The complexity is log N
Now, I’ve used O(n) notation above. And that’s the talk of this part. So, what is it?
Big Oh
So, complexity! Ever so weird word! The next image shows a complexity chart:
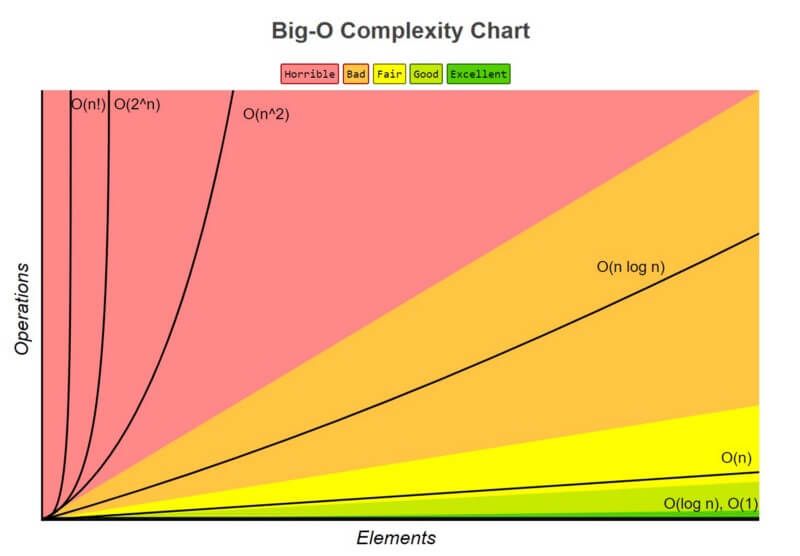
Now, we can see a bunch of stuff in there. From best to worst:
- O(1) as excellent
- O(log n) as good
- O(n) as fair
- O(n log n) as bad
- O(n^2), O(2^n) and O(n^m), as horrible
Well, let’s put some more examples:
- Accessing array on an index is O(1).
- It doesn’t matter if I do
[1,2,3][0]or[1,2,3][2]. - It will still take the same time.
- It’s constant in all circumstances
- It doesn’t matter if I do
- Finding something by binary search is O(log n). The worst time it takes is the logarithm of n.
- Example is binary search on sorted array
- In worst case, it takes N steps
- Finding something in array with regular search is O(n)
- Example is regular search on unsorted array
- In worst case, it will take N steps
- Sorting an array properly is O(n log n)
- A sorting algorithm will traditionally take O(n log n) steps
- Sorting an array by comparing all individual items is O(n^2)
- We will have to iterate through all elements twice
- Recursive algorithms are often O(2^n)
- Given a number N, it will perform it’s operation on N, N-1, N-2, N-3
- For example, when I write a fibonacci function
Intermezzo
So, we’ve learned a little about Big Oh. The gist of it is, it’s a math way of saying “Hey, this takes some time”.
Now, why do we care about something taking time? Well, imagine that your’e developing Facebook. You have A LOT of data. If you store it in a bad way, your product will be so slow it becomes unusable. Would you still use Facebook if it took 10 mins to send a message? Probably not.
So, what can we do with it? Well, we use it to speed up code.
As I mentioned before, we have a sorting algorithm.
- If we use quicksort, it’s O(n log n)
- If we use bubble sort, it’s O(n^2)
- We can immediately tell that bubble sort is better
So, all in all, it’s just a short way of saying how efficient an algorithm is. And if we deem it too slow, then we can improve.
Speeding up code with Big Oh
So, how can we use Big Oh to speed up our code?
Well, we can’t use Big Oh itself. What we choose is using:
- A better data structure, or
- A better algorithm
So, let’s consider we’re searching in a sorted array:
const arr = Array.from({length: 100}, (v, k) => k);Let’s consider we’re searching for number 60.
- If we went from start to end, it’d take 60 steps
- If we went from end to start, it’d take 40 steps
- Worst case condition, it will always take 100 steps
So, let’s use binary search!
Array.prototype.binarySearch = function (what) {
let lowerBound = 0;
let upperBound = this.length;
while (upperBound >= lowerBound) {
const middle = Math.floor((upperBound - lowerBound) / 2 + lowerBound);
if (this[middle] === what) return what;
if (this[middle] < what) lowerBound = middle;
else upperBound = middle;
}
return undefined;
};Now, with this, we’re basically looking at every middleth element. The most it can take is log(100). Or 7 steps (round up). Can we use this always? Of course not. We can do it only on sorted arrays! But it’s a great example of usefulness!
One thing to note here is the clever way with indices. Imagine the following code to do the search:
Array.prototype.binarySearch = function (what) {
let _this = this;
while (_this.length > 1) {
const middle = Math.floor(_this.length / 2);
if (_this[middle] === what) return what;
if (_this[middle] < what) _this = _this.slice(middle);
else _this = _this.slice(0, middle)
}
return _this[0] == what ? what : undefined;
};While it seemingly does the same thing, notice the slice method. Slicing an array is actually a
JavaScript implementation of a slicing algorithm, which would take some time. So, to actually be efficient, we’d
have to perform the clever index play.
How would we perform the sort? Well, I’ve mentioned bubble sort and quick sort. Let me quickly create bubble sort, because it’s very easy, but also very slow:
Array.prototype.bubbleSort = function () {
let numberOfSorted = 0;
let sorted = false;
while (!sorted) {
const unsortedUntil = this.length - numberOfSorted;
sorted = true;
for (let i = 0; i < unsortedUntil; i++) {
const previous = this[i];
const next = this[i + 1];
if (previous > next) {
this[i] = next;
this[i + 1] = previous;
sorted = false;
}
}
numberOfSorted++;
}
};
arr.bubbleSort();In this case, we start with reversed array. Then, we compare each items, and if they are out of order, we sort them
And that’s it. Once we apply this bubble sort ONCE, all subsequent searches will be fast. And that’s the importance.
Speeding up code without Big Oh
Now, in the previous example, we’ve sped up the search by applying it on a sorted array. We’ve:
- Sorted the array first
- Performed all subsequent searches effectively
Without sorting, all searches would be O(n). With it, all searches are O(log n).
Now, it may very well be the case that 2 algorithm of same “Oh Rank” would not have the same speed.
Consider the following example:
// first
for (let i = 0; i < 1_000_000; i++) {
const j = i;
const c = i;
console.log(i);
}
// second
for (let i = 0; i < 1_000_000; i++) {
console.log(i);
}In the example, we have 2 for loops. But the first one is thrice as fast, because it performs less operations. However, both would be considered O(n). That’s because constants are ignored.
If something takes O(3 * n) - such as the first example - it’d be still considered O(n).
That’s also the reason why O(1) doesn’t mean it always takes 1 step. It means that no matter the circumstances, it’ll always be equally fast (or slow). For an example of this, you can think of objects:
const a = { a: 1, b: 2, c: 3 };
const b = { c: 3 }
const res1 = a['c'];
const res2 = b['c'];In the above example, the res1 and res2 retrievals take the same time.
With that in mind, I’ve previously done bubble sort. Let me quickly show selectionSort:
const arr = Array.from({ length: 100 }, (v, k) => k).reverse();
Array.prototype.selectionSort = function() {
for (let i = 0; i < this.length; i++) {
for (let j = i + 1; j < this.length; j++) {
let prev = this[i];
let curr = this[j];
if (prev > curr) {
this[i] = curr;
this[j] = prev;
}
}
}
}
arr.selectionSort();If we compare the two, we basically have:
- bubbleSort, who compares 2 adjacent items on the entire array until it is sorted
- selectionSort, where an item is compared to all subsequent items.
In other words:
- selectionSort will first find the element to 0th index, then first, up until nth index.
- bubbleSort is opposite - it will first make sure the biggest element is on the end
With that in mind, we can actually say that when an array is sorted ascending, bubble sort does nothing!
However, selectionSort will still perform ~5k operations.
So, even though both are O(n^2), you can choose one for better performance, depending on its usage.
I want to make one thing absolutely clear - none of these sorts are used nowadays as they are slow. However, they are good examples of how something can be done it different ways with same “Oh Rank”, but have different speeds depending on the usage.
Summary
So, we’re at the end of Big Oh! The key takeaway about Big Oh is:
- It’s valuable for getting an idea how fast something is
- The real run can actually be slower or faster, as it ignores constants
- 6n operations is O(n)
- 6n^2 operations is O(n^2)
To get an idea of common use cases and algorithms used:
- Word builder - nested loops
- O(N^M)
- N^2 with 2 letters, N^3 with 3 letters and so on
- Palindrome - While until index is in middle
- O(N)
- Actually N / 2
- Password Cracker - (a..z, aa..zz)
- With only alphabet, O(26^N)
- Extremely slow
Furthermore, we basically have 3 ways to optimize code:
- Wisely choosing data structure (Allows for better algorithms for specific problems)
- Wisely choosing algorithm (Allows for better Big Oh Rank)
- Performing only necessary steps (Reducing number of steps yet retaining Big Oh Rank)
References

